Page 9 - LAPLACE TRANSFORM

1.2 Laplace Transform Formula

Laplace transform is the integral transform of the given derivative function with
real variable t to convert into a complex function with variable s. For t ≥ 0, let f(t)
be given and assume the function satisfies certain conditions to be stated later on.

The formula for the Laplace transform of f(t), represented by L f(t) or F(s) is as
follows: Suppose that is a function that is defined for all positive t values.

∞
t
F ( ) = ∫ e − st f ()dt
s
0

whenever the improper integral converges.

Standard notation : Where the notation is clear, we will use an uppercase letter to
indicate the Laplace Transform, example , L(f; s)=F(s).

The Laplace transform we defined is sometimes called the one-sided Laplace
Transform. The integral in the two-sided version varies from −∞ to ∞.

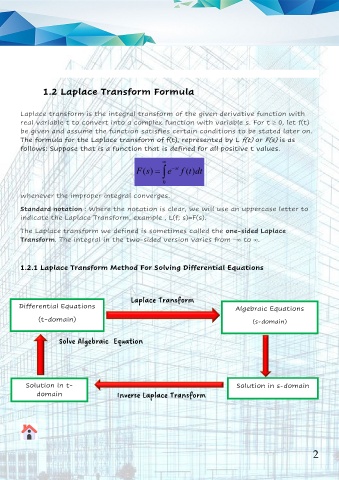
1.2.1 Laplace Transform Method For Solving Differential Equations

Laplace Transform
Differential Equations Algebraic Equations

(t-domain) (s-domain)

Solve Algebraic Equation

Solution in t- Solution in s-domain
domain
Inverse Laplace Transform

2